1.2 선형대수학 필요한 만큼만 배우기

해당 글은 코드잇 강의를 참고하여 작성되었습니다.

- 일차식과 일차 함수

• 선형대수학 : 일차식이나 일차 함수를 공부하는 학문
• 일차식 : 가장 높은 차수가 1인 다항식 
• 함수 : x에 따라 y가 정해지는 식

 

- 일차 함수 표기법

• f(x0,x1,...)=a0x0 + a1x1 + ...

 

- 행렬과 벡터

• 행렬(Matrix) : 수를 직사각형 형태로 나열한 것 → 가로=행, 세로=열
• ex) A12, A31 ...​
• 벡터(Vector) : 행이 하나밖에 없거나 열이 하나밖에 없는 것(기본적으로 벡터=열벡터)
• ex) a1, b3

 

- 행렬 연산

• np.array로 2차원 배열을 만든다.
• np.zeros는 괄호를 1개 더 사용한다.

  

 

- numpy로 행렬 연산하기

• 행렬 덧셈 : 같은 위치의 원소끼리 더한다. (같은 차원의 행렬만 가능)
• 행렬 곱셈 
  • 스칼라곱 : 각 원소에 상수를 곱한다.
  • 내접곱 :

    

    m x n인 행렬 A와 n x p인 행렬 B는 곱셈가능(n이 같기 때문)결과 = m x p 행렬교환법칙이 성립하지 않는다    A @ B 
  • 요소별 곱하기 : 각 행렬의 값끼리 곱하기(같은 차원의 행렬만 가능)

    

 

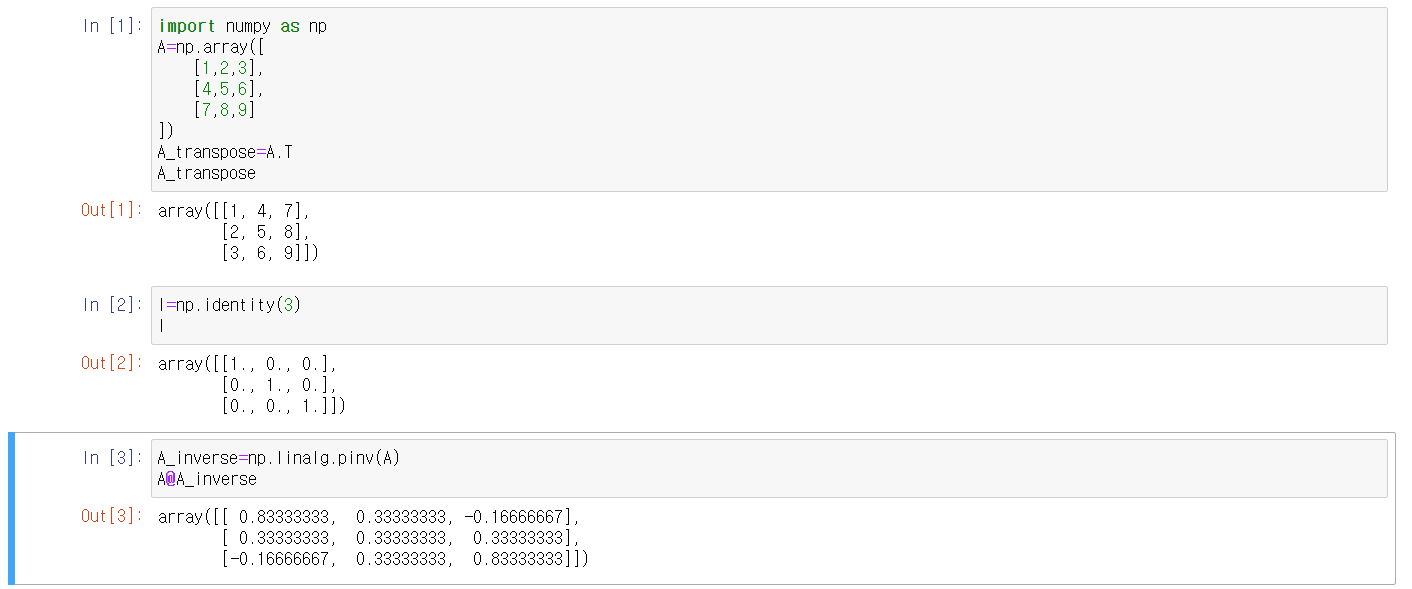
- 전치행렬, 단위 행렬, 역행렬

• 전치행렬(transposed matrix)

  

• 단위행렬(identity matrix) : 항상 정사각형 → ×1과 같은 역할

  

• 역행렬(inverse matrix) : 곱했을 때 단위행렬이 나오도록 만드는 행렬 → 모든행렬에 역행렬이 있는 것은 아니다.

  

 

- 선형대수학과 행렬/벡터

• 선형 시스템을 행렬과 벡터로 쉽게 표현가능하다.

 

- 선형대수학이 머신 러닝에 필요한 이유

• 머신 러닝을 할 때는 데이터를 일차식에 사용하는 경우가 많다.
• 행렬을 이용하면 정돈된 형태로 효율적이게 계산을 할 수 있다.
• 선형 대수학은 일차식, 일차 함수, 행렬, 벡터를 다루는 학문이기 때문에 필수이다.